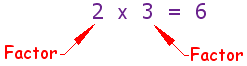Maths Blog for Year 10 BVIS
I. Number:
A. Chapter 1
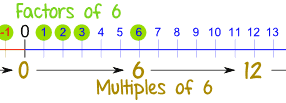
1. Multiples of whole numbers.
2. Factors of whole numbers.
3. Prime numbers.

4.Square numbers and roots.
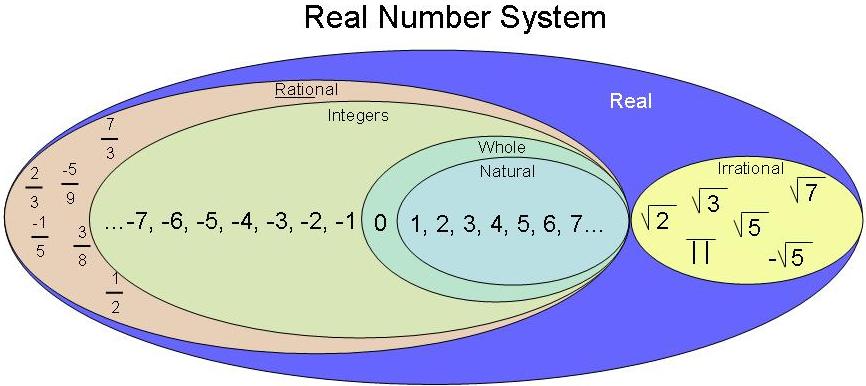
5. Real numbers.
B. Chapter 2
1.Fractions, decimals and percentages.
2.Calculating a percentage.

3. Increasing or decreasing quantities by a percentage.
For examples:
a. Increase $6 by 5%
5% of $6 : (5 : 100) x 6 = $0.30
=> $6 + $0.30 = $6.30
b. Increase $6 by 5%
=> $6 x 1.05 = $6.30
For examples:
a. Decrease $8 by 4%
4% of $8: (4 : 100) x 8 = $0.32
=> $8 - $0.32 = $7.68
b. Decrease $8 by 4%
=> $8 x 0.96 = $7.68
4. Simple interest and compound interest.

5. Reverse percentage.

C. Chapter 3
1. The four rules.
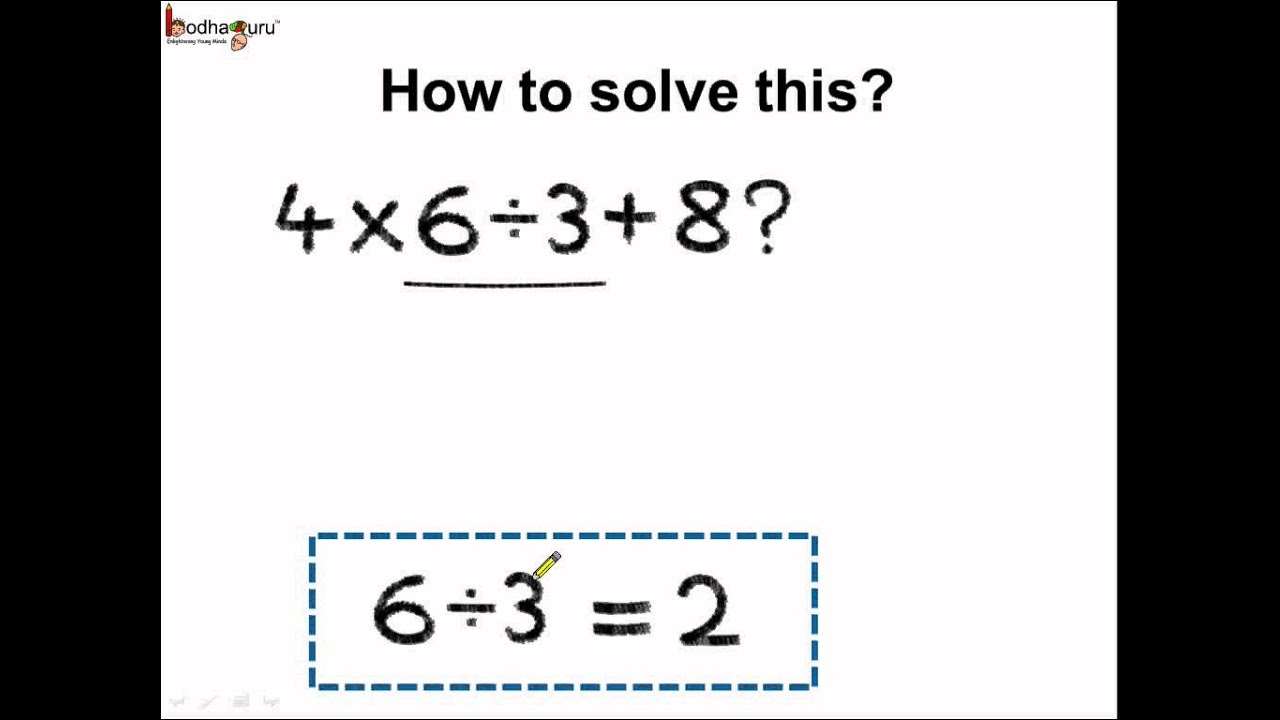
D. Chapter 4
1. Directed numbers.

E. Chapter 5
1. Squares and square roots.
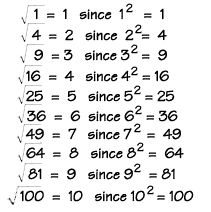
2. Cubes and cube roots.
F. Chapter 6 

1. Inequalities.
\
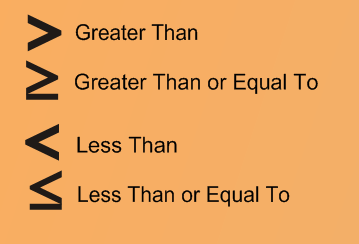
2. Sets.

3. Venn diagram.

G. Chapter 7
1. Ratio

2. Increases and decreases using ratios
Increase 20 in the ratio 3 : 2.
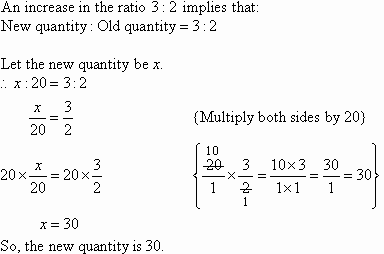
Decrease 32 in the ratio 3 : 4.
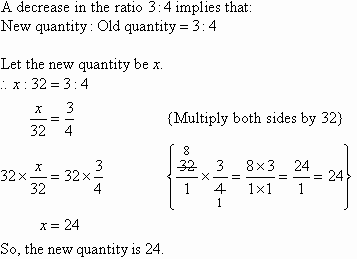
Solution:
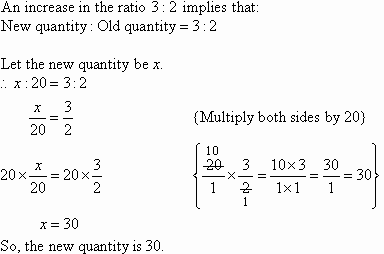
Decrease 32 in the ratio 3 : 4.
Solution:
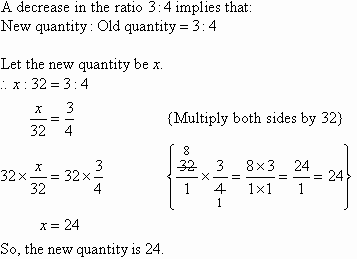
3. Direct proportion
If 10 calculators cost $120, how much will 8 calculators cost?
$120 : 10 = $12 / a calculator
=> $12 x 8 = $96 / 8 calculators
4. Inverse proportion
Example: 4 people can paint a fence in 3 hours.
How long will it take 6 people to paint it?
We can use:
t = k/n
Where:
- t = number of hours
- k = constant of proportionality
- n = number of people
We know that t = 3 when n = 4
3 = k/4
3 × 4 = k × 4 / 4
12 = k
k = 12
So now we know:
t = 12/n
And when n = 6:
t = 12/6 = 2 hours
So 6 people will take 2 hours to paint the fence.
How many people are needed to complete the job in half an hour?
½ = 12/n
n = 12 / ½ = 24
So it needs 24 people to complete the job in half an hour.
H. Chapter 8
1. Rounding whole numbers

2. Rounding decimals

3. Rounding to significant figures

4. Upper and lower bounds

5. Upper and lower bounds for calculations
Question
A hoist can lift 1,600 kg, given to 2 significant figures. It is being used to load boxes that weigh 48 kg to the nearest kg.
How many boxes can the hoist safely lift?
Solution
For a quick recap on significant figures see the section Significant figures.
For safety we need to think about the lower limit for the hoist and the higher limit for each box.
The lower limit for the hoist is 1,550 kg.
The higher limit for each box is 48.5 kg.
1550 ÷ 48.5 = 31.9….
Even though this is very close to 32, the hoist can only lift 31 boxes safely.
I. Chapter 9
1. Standard form
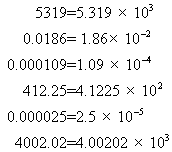
2. Calculating with standard form
Algebra
A. Chapter 1
1. Simplifying expressions
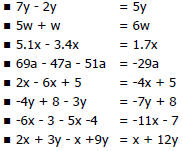
2. Expanding brackets

3. Factorisation

4. Multiplying two brackets

5. Quadratic factorisation

6. Algebraic equations

B. Chapter 2
1. Solving linear equations
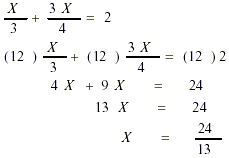
2. Setting up equations

3. Solving quadratic equations by factorisation
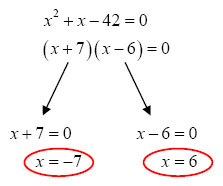
4. Solving quadratic equations by the quadratic formuala
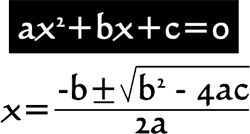
5. Solving quadratic equations by completing the square

6. Simultaneous equations
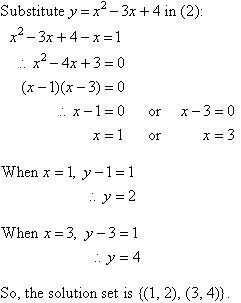
7. Solving inequalities

C. Chapter 3
1. Conversion graphs

2. Travel graphs

3. Speed - time graphs

D. Chapter 4
1. Drawing straight line graphs
2. The equation y = mx + x

3. Parallel lines

4. Points and lines
E. Chapter 5
1. Quadratic graphs

F. Chapter 6
1. Number sequences

2. The nth term of a sequence

3. General rules from patterns
G. Chapter 7
1. Using indices

2. Negative indices

3. Multiplying and dividing with indices


4. Fractional indices

H. Chapter 8
1. Direct variation

2. Inverse variation

I. Chapter 9
1. Graphical inequalities
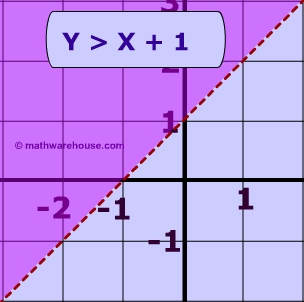
2. More than one inequality

3. Linear programming

J. Chapter 10
1. Function notation

2. Inverse functions
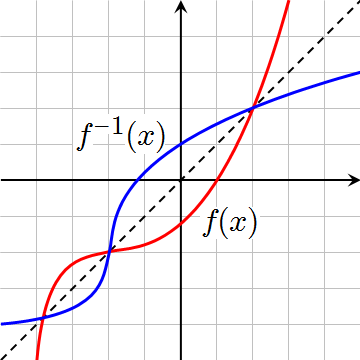
3. Composite functions

4. More about composite functions
Geometry and trigonometry
A. Chapter 1
1. Angle facts
2. Parallel lines

3. Angles in a triangle
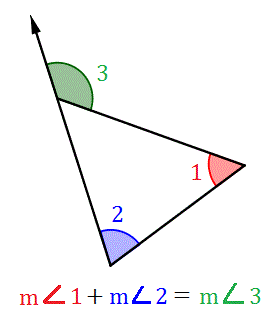
4. Angles in a quadrilateral
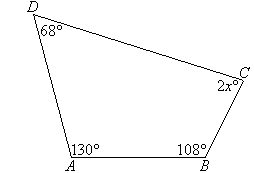
5. Regular polygons
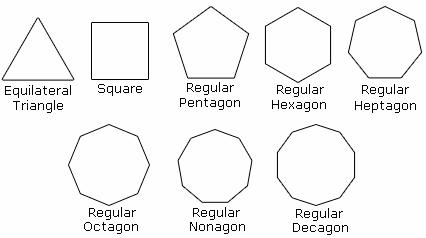
6. Irregular polygons

7. Tangents and diameters

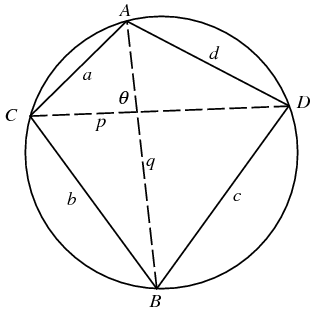
8. Angles in a circle

9. Cyclic quadrilaterals
B. Chapter 2
1. Measuring and drawing angles

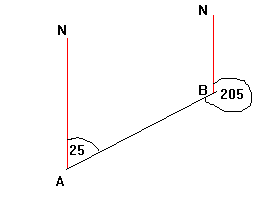
2. Bearings
3. Nets

4. Congruent shapes

5. Similar shapes
6. Areas of similar triangles

7. Areas and volumes of similar shapes

C. Trigonometry
1. Pythagoras' theorem

2. Trigonometric ratios

3. Calculating angles

4. Using sine, cosine and tangent functions

5. Which ratio to use

6. Sine and cosine of obtuse angles

7. The sine rule and the cosine rule

8. Using sine to find the area of a triangle